Research Highlights
AquaticVision: Benchmarking Visual SLAM in Underwater Environment with Events and Frames
We propose the first underwater dataset that simultaneously incorporates event camera data, traditional camera frames, and IMU measurements. Furthermore, we release groundtruth trajectories tracked by a motion capture system, enabling researchers to validate the localization accuracy and performance of their algorithms in underwater scenes. The dataset is categorized into "easy" and "hard" classes, where sequences in the easy class were collected under good water quality and lighting conditions, while sequences in the hard class include special underwater conditions such as low light, high dynamic range (HDR), and turbidity. Furthermore, based on this dataset, we evaluated mainstream frame-based visual SLAM algorithms and a state-of-the-art event-based SLAM algorithm in underwater scenarios. The analysis of advantages and limitations of event camera points to potential future directions for underwater SLAM research. We hope this dataset can enable researchers to validate the localization accuracy and performance of their algorithms in underwater environments.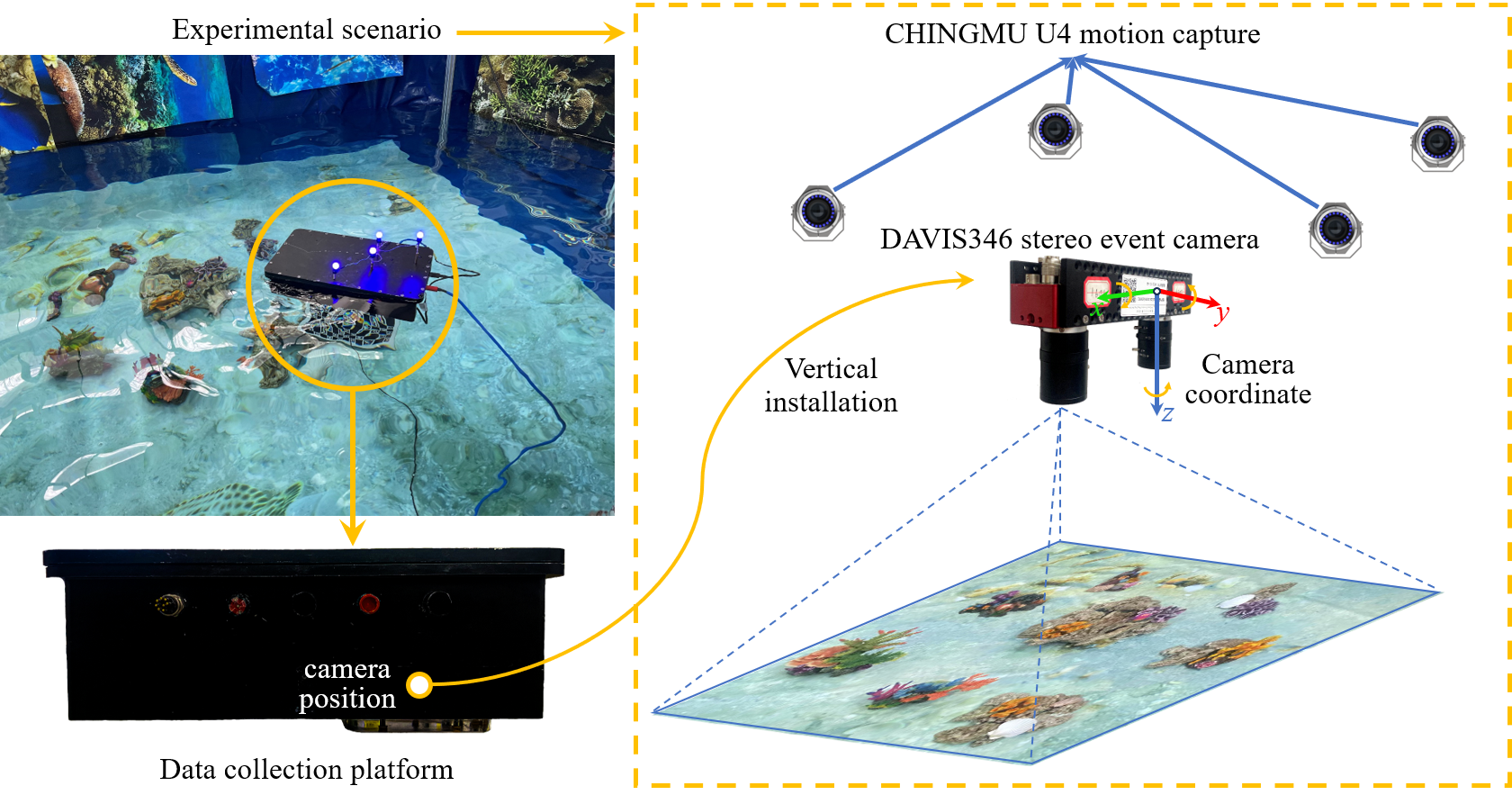

Dataset Project Page: https://sites.google.com/view/aquaticvision-lias
Paper: https://arxiv.org/abs/2505.03448
Citation:
@article{peng2025aquaticvision,
title={AquaticVision: Benchmarking Visual SLAM in Underwater Environment with Events and Frames},
author={Peng, Yifan and Hong, Yuze and Hong, Ziyang and Chui, Apple Pui-Yi and Wu, Junfeng},
journal={arXiv preprint arXiv:2505.03448},
year={2025}
}BESTAnP: Bi-Step Efficient and Statistically Optimal Estimator for Acoustic-n-Point Problem
We present BESTAnP, a novel algorithm for estimating 2D forward-looking sonar pose using 3D-2D point correspondences. Our two-step approach separates translation and rotation estimation, achieving the first closed-form solution for full six-degree pose in sonar localization. BESTAnP demonstrates 10x faster performance than existing methods while maintaining comparable accuracy, making it suitable for real-time applications on resource-limited platforms. Successful integration with sonar-based odometry validates its practical effectiveness in trajectory estimation.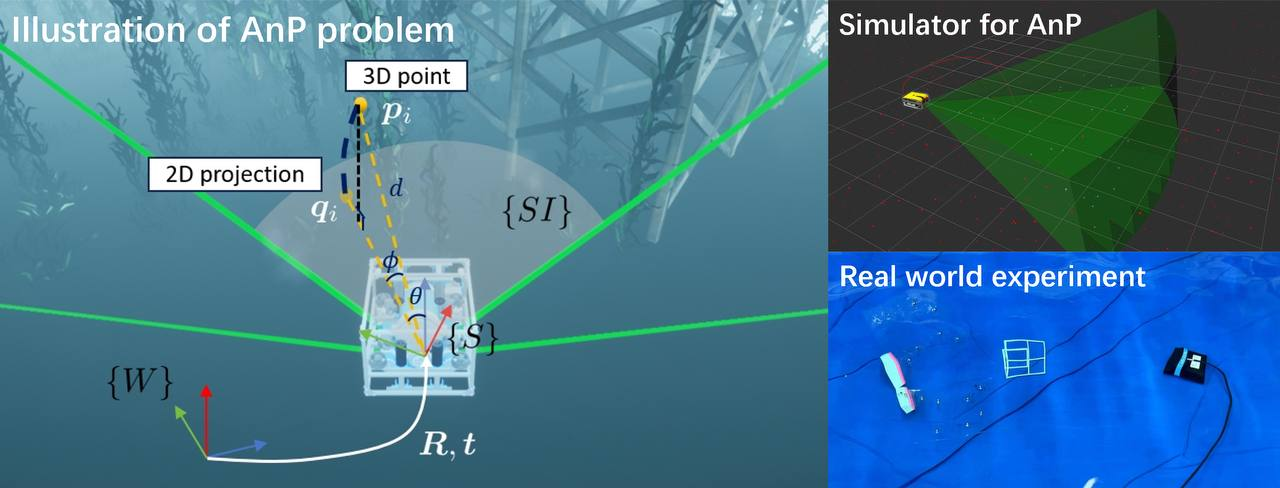 Authors: Wenliang Sheng, Hongxu Zhao, Lingpeng Chen, Guangyang Zeng, Yunling Shao, Yuze Hong, Chao Yang, Ziyang Hong, and Junfeng Wu
Authors: Wenliang Sheng, Hongxu Zhao, Lingpeng Chen, Guangyang Zeng, Yunling Shao, Yuze Hong, Chao Yang, Ziyang Hong, and Junfeng WuPaper: https://arxiv.org/abs/2411.17521
Code, Dataset and More Details: https://github.com/LIAS-CUHKSZ/
Citation:
@article{sheng2024bestanpbistepefficientstatistically,
title={BESTAnP: Bi-Step Efficient and Statistically Optimal Estimator for Acoustic-n-Point Problem},
author={Wenliang Sheng and Hongxu Zhao and Lingpeng Chen and Guangyang Zeng and Yunling Shao and Yuze Hong and Chao Yang and Ziyang Hong and Junfeng Wu},
journal={arXiv preprint arXiv:2411.17521},
year={2024}
}Efficient Planar Pose Estimation via UWB Measurements
We investigate planar pose estimation using only UWB range measurements. We prove the excellent property of a two-step scheme, which says we can refine a consistent estimator to be asymptotically efficient by one step of Gauss-Newton iteration. Grounded on this result, we design the GN-ULS estimator, which reduces the computation time significantly compared to previous methods and presents the possibility of using only UWB for real-time state estimation.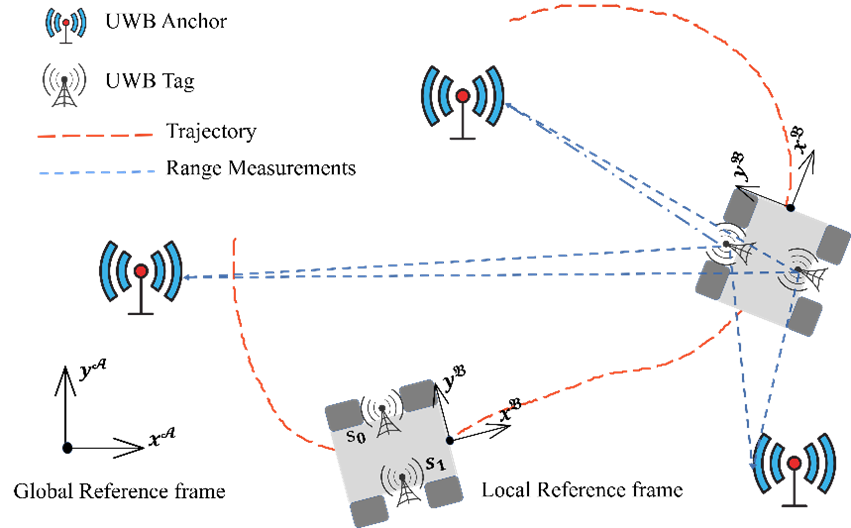

Paper: https://arxiv.org/abs/2209.06779
Video: https://www.bilibili.com/video/BV1Fg4y1t786
Code, Dataset and More Details: https://github.com/SLAMLab-CUHKSZ/Efficient-Pose-Estimation-via-UWB-measurements
Citation:
@article{jiang2022efficient,
title={Efficient Planar Pose Estimation via UWB Measurements},
author={Jiang, Haodong and Wang, Wentao and Shen, Yuan and Li, Xinghan and Ren, Xiaoqiang and Mu, Biqiang and Wu, Junfeng},
journal={arXiv preprint arXiv:2209.06779},
year={2022}
}Closed-Form Error Propagation on SEn(3) Group for Invariant EKF With Applications to VINS
Pose estimation is important for robotic perception, path planning, etc. Robot poses can be modeled on matrix Lie groups and are usually estimated via filter-based methods. In this work, we establish the closed-form formula for the error propagation for the Invariant extendedKalmanfilter (IEKF) in the presence of random noises and apply it to vision-aided inertial navigation. Moreover, we use the theoretic results to add the compensation parts for IEKF.We evaluate our algorithms via numerical simulations and experiments on the OPENVINS platform. Both simulations and the experiments performed on the public EuRoC MAV datasets demonstrate that our algorithm in particular parameters settings outperforms some state-of-art filter-based methods such as the quaternion-based EKF, first estimates Jacobian EKF, etc. The techniques of choice on the parameters are worth further investigating.Authors: Xinghan Li, Haodong Jiang, Xingyu Chen, He Kong, and Junfeng Wu
Video: https://youtu.be/AnxM2E0133Q
Citation:
@ARTICLE{Xinghan2022,
author={Li, Xinghan and Jiang, Haodong and Chen, Xingyu and Kong, He and Wu, Junfeng},
journal={IEEE Robotics and Automation Letters},
title={Closed-Form Error Propagation on {$SE_n(3)$} Group for Invariant EKF With Applications to VINS},
year={2022},
volume={7},
number={4},
pages={10705-10712},
doi={10.1109/LRA.2022.3194684}
}CPnP: Consistent Pose Estimator for Perspective-n-Point Problem with Bias Elimination
The Perspective-n-Point (PnP) problem has been widely studied in both computer vision and photogrammetry societies. With the development of feature extraction techniques, a large number of feature points might be available in a single shot. It is promising to devise a consistent estimator, i.e., the estimate can converge to the true camera pose as the number of points increases. To this end, we propose a consistent PnP solver, named CPnP, with bias elimination. Specifically, linear equations are constructed from the original projection model via measurement model modification and variable elimination, based on which a closed-form least-squares solution is obtained. We then analyze and subtract the asymptotic bias of this solution, resulting in a consistent estimate. Additionally, Gauss-Newton (GN) iterations are executed to refine the consistent solution. Our proposed estimator is efficient in terms of computations—it has O(n) time complexity. Simulations and real dataset tests show that our proposed estimator is superior to some well-known ones for images with dense visual features, in terms of estimation precision and computing time.Authors: Guangyang Zeng, Shiyu Chen, Biqiang Mu, Guodong Shi, and Junfeng Wu
Paper: https://arxiv.org/abs/2209.05824
Video: to be added
Code: https://github.com/SLAMLab-CUHKSZ/CPnP-A-Consistent-PnP-Solver (Matlab/Python/C++ codes for the implementation of the proposed CPnP solver)
Citation:
@inproceedings{ zeng2023cpnp,
title={CPnP: Consistent Pose Estimator for Perspective-n-Point Problem with Bias Elimination},
author={Zeng, Guangyang and Chen, Shiyu and Mu, Biqiang and Shi, Guodong and Wu, Junfeng},
booktitle={IEEE International Conference on Robotics and Automation (ICRA)},
pages={},
year={2023},
organization={IEEE}
}Global and Asymptotically Efficient Localization from Range Measurements
We consider the range-based localization problem, which involves estimating an object’s position by using m sensors, hoping that as the number m of sensors increases, the estimate converges to the true position with the minimum variance. We show that under some conditions on the sensor deployment and measurement noises, the LS estimator is strongly consistent and asymptotically normal. However, the LS problem is nonsmooth and nonconvex, and therefore hard to solve. We then devise realizable estimators that possess the same asymptotic properties as the LS one. These estimators are based on a two-step estimation architecture, which says that any √m-consistent estimate followed by a one-step Gauss-Newton iteration can yield a solution that possesses the same asymptotic property as the LS one. The keypoint of the two-step scheme is to construct a √m-consistent estimate in the first step. In terms of whether the variance of measurement noises is known or not, we propose the Bias-Eli estimator (which involves solving a generalized trust region subproblem) and the Noise-Est estimator (which is obtained by solving a convex problem), respectively. Both of them are proved to be √m-consistent. Moreover, we show that by discarding the constraints in the above two optimization problems, the resulting closed-form estimators (called Bias-Eli-Lin and Noise-Est-Lin) are also √m-consistent. Plenty of simulations verify the correctness of our theoretical claims, showing that the proposed two-step estimators can asymptotically achieve the Cramer-Rao lower bound.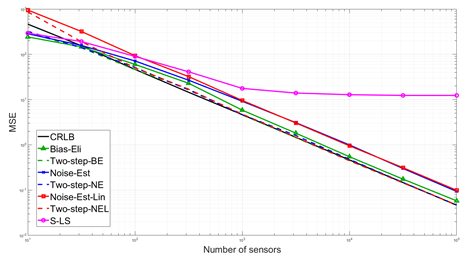
Paper: https://ieeexplore.ieee.org/abstract/document/9855392
Citation:
@article{zeng2022global,
title={Global and asymptotically efficient localization from range measurements},
author={Zeng, Guangyang and Mu, Biqiang and Chen, Jiming and Shi, Zhiguo and Wu, Junfeng},
journal={IEEE Transactions on Signal Processing},
volume={70},
pages={5041–5057},
year={2022},
publisher={IEEE}
}Localizability with Range-Difference Measurements: Numerical Computation and Error Bound Analysis
This project studies the localization problem using noisy range-difference measurements, or equivalently time difference of arrival (TDOA) measurements. There is a reference sensor, and for each other sensor, the TDOA measurement is obtained with respect to the reference one. By minimizing the sum of squared errors, a nonconvex constrained least squares (CLS) problem is formulated. In this work, we focus on devising an algorithm to seek the global minimizer of the CLS problem, hoping that the numerical solution meets some precision requirement in terms of relative error. Based on the Lagrange multiplier method, we first branch the feasible Lagrange multiplier set into several subsets and develop a workflow in terms of if-then-else control structure to seek the global minimizer by searching for the optimal Lagrange multiplier. The execution order is carefully organized so that it is in line with the general principle of putting the flow that one normally understands to be executed first. We then dive into detailed searching methods in different cases and conduct computational error analysis, giving the error bound on the Lagrange multiplier, when we search for it, to meet the precision requirement on an approximate solution. Based on the above achievements, a programmable global minimizer seeking algorithm is proposed for the CLS problem. Simulations and experimental tests on a public dataset demonstrate the effectiveness of the proposed algorithm.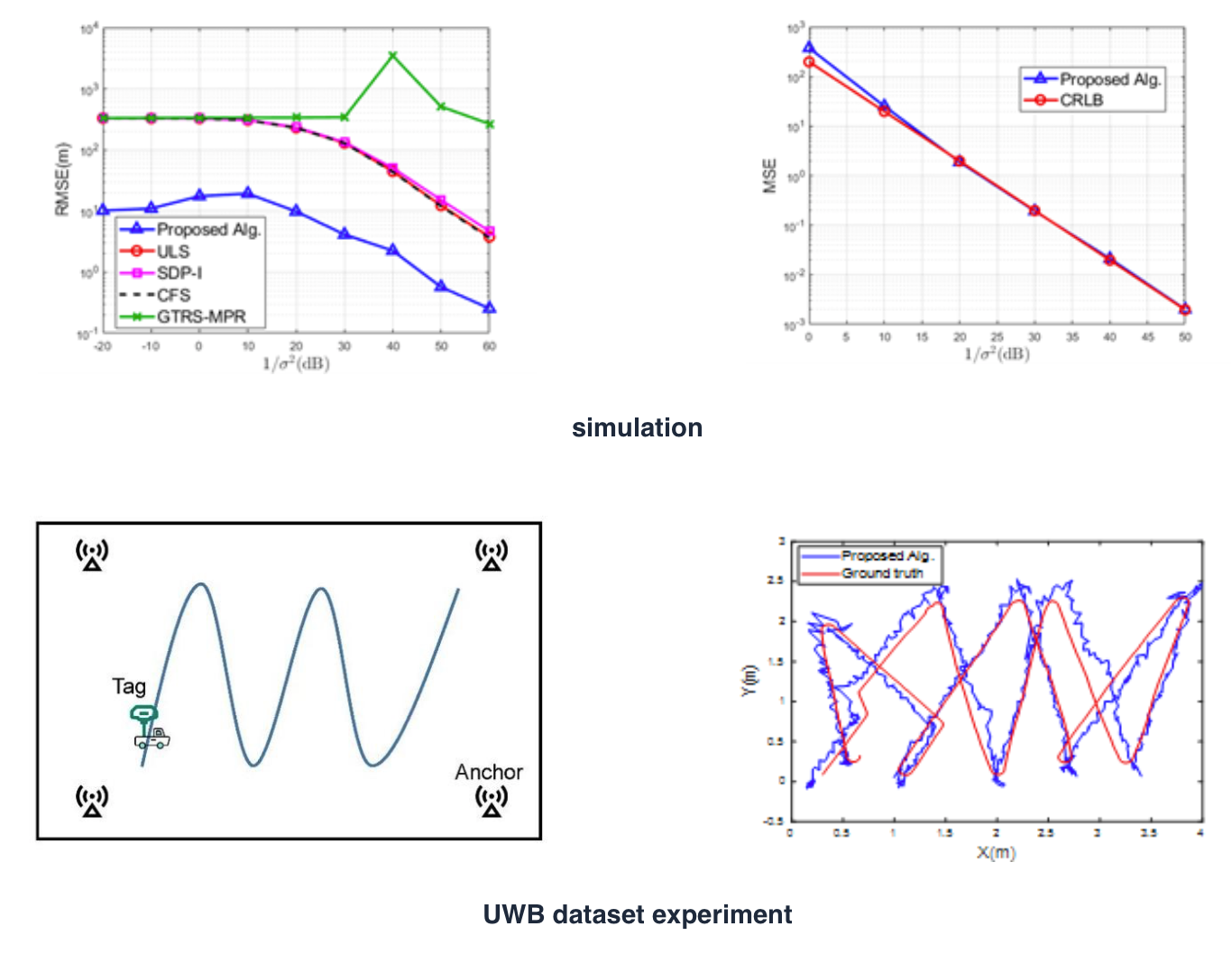 Authors: Guangyang Zeng, Biqiang Mu, Jieqiang Wei, Wing Shing Wong, and Junfeng Wu
Authors: Guangyang Zeng, Biqiang Mu, Jieqiang Wei, Wing Shing Wong, and Junfeng WuCode: https://guangyangzeng.github.io/publications/ (Matlab codes for the implementation of the proposed CLS solver)
Paper: https://ieeexplore.ieee.org/abstract/document/9760067
Citation:
@article{zeng2022localizability,
title={Localizability with range-difference measurements: Numerical computation and error bound analysis},
author={Zeng, Guangyang and Mu, Biqiang and Wei, Jieqiang and Wong, Wing Shing and Wu, Junfeng},
journal={IEEE/ACM Transactions on Networking},
volume={30},
number={5},
pages={2117–2130},
year={2022},
publisher={IEEE}
}Low-complexity Distributed Detection with One-bit Memory Under Neyman-Pearson Criterion
We consider a multi-stage distributed detection scenario, where $n$ sensors and a fusion center (FC) are deployed to accomplish a binary hypothesis test. At each time stage, local sensors generate binary messages, assumed to be spatially and temporally independent given the hypothesis, and then upload them to the FC for global detection decision making. We suppose a one-bit memory is available at the FC to store its decision history and focus on developing iterative fusion schemes. We first visit the detection problem of performing the Neyman-Pearson (N-P) test at each stage and give an optimal algorithm, called the oracle algorithm, to solve it. Structural properties and limitation of the fusion performance in the asymptotic regime are explored for the oracle algorithm. We notice the computational inefficiency of the oracle fusion and propose a low-complexity alternative, for which the likelihood ratio (LR) test threshold is tuned in connection to the fusion decision history compressed in the one-bit memory. The low-complexity algorithm greatly brings down the computational complexity at each stage from O(4^n) (worst case) to O(n). We show that the proposed algorithm is capable of converging exponentially to the same detection probability as that of the oracle one. Moreover, the rate of convergence is shown to be asymptotically identical to that of the oracle algorithm. Finally, numerical simulations and real-world experiments demonstrate the effectiveness and efficiency of our distributed algorithm.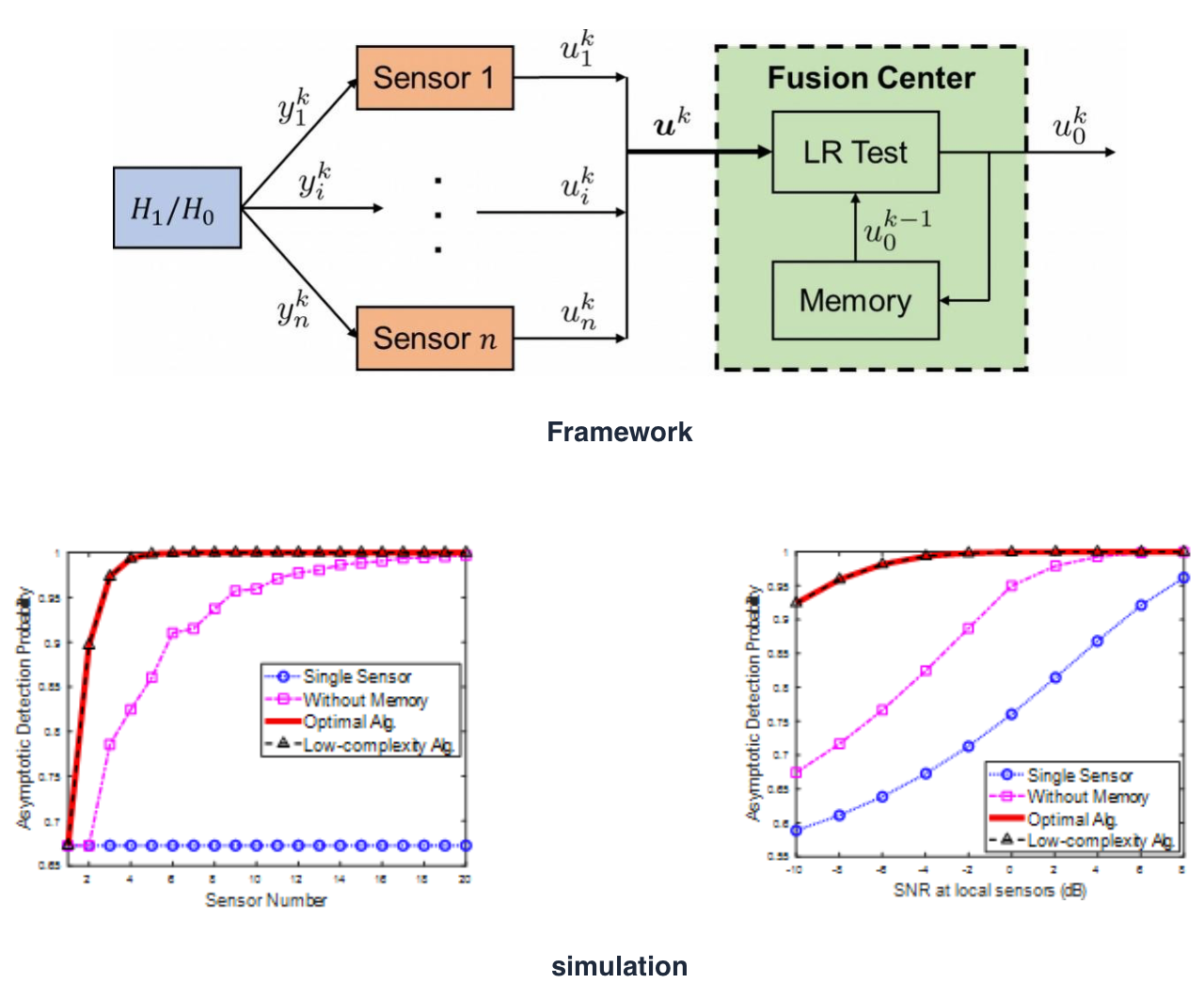 Authors: Guangyang Zeng, Xiaoqiang Ren, and Junfeng Wu
Authors: Guangyang Zeng, Xiaoqiang Ren, and Junfeng WuPaper: https://ieeexplore.ieee.org/abstract/document/9672725
Citation:
@article{zeng2022low,
title={Low-complexity distributed detection with one-bit memory under Neyman–Pearson criterion},
author={Zeng, Guangyang and Ren, Xiaoqiang and Wu, Junfeng},
journal={IEEE Transactions on Control of Network Systems},
volume={9},
number={1},
pages={2–13},
year={2022},
publisher={IEEE}
}MaskedXGBoost: Privacy-preserving Federated XGBoost with Differential Privacy Guarantee
We propose a variant of Vertical Federated XGBoost with a differential privacy guarantee: MaskedXGBoost. We build well-constructed noise to perturb the intermediate information to protect privacy, with nearly lossless accuracy and much lower overhead than encryption-based techniques. We build a label inference attacker to evaluate our approach’s privacy-preserving empirically besides theoretical privacy analysis. The utility, efficiency, and empirical privacy of the protocol are verified on multiple datasets.Authors: Bokang Zhang, Shuaiting Huang, Zhikun Zhang, Yang Liu, Junfeng Wu, Yuxiao Zhou, and Lihao Zheng
Minimum-Degree Distributed Graph Filter Design
We establish fundamental connections between local response of shifting at a node, concerned in the GSP field, and the observability of the system, investigated in control theory. Specifically, by introducing a notion of observable graph frequencies to a node, we show that the output signals (observations) at a node only contain the spectral components of its so-called observable graph frequencies. We use low-pass graph filters as an example to illustrate the application of our proposed Algorithm 1 in computing a consensus value for a sensor network. We randomly generate an undirected graph of 7 nodes and treat the Laplacian matrix as the operator A with specific value. We compute the consensus value using the proposed node-variant GF and a minimum number of observations.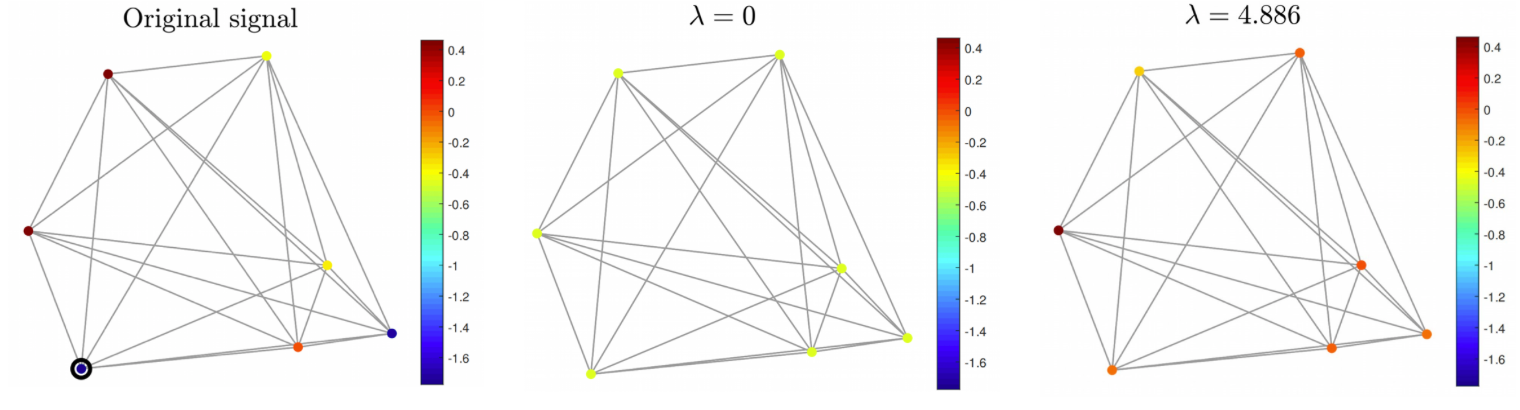 Authors: Kemi Ding, Junfeng Wu, and Lihua Xie
Authors: Kemi Ding, Junfeng Wu, and Lihua XiePaper: https://ieeexplore.ieee.org/abstract/document/9335536
Citation:
@ARTICLE{9335536,
title={Minimum-Degree Distributed Graph Filter Design},
author={Ding, Kemi and Wu, Junfeng and Xie, Lihua},
journal={IEEE Transactions on Signal Processing},
volume={69},
number={},
pages={1083-1096},
year={2021},
doi={10.1109/TSP.2021.3053643}}Links
Bilibili: https://space.bilibili.com/1412522312GitHub: https://github.com/LIAS-CUHKSZ